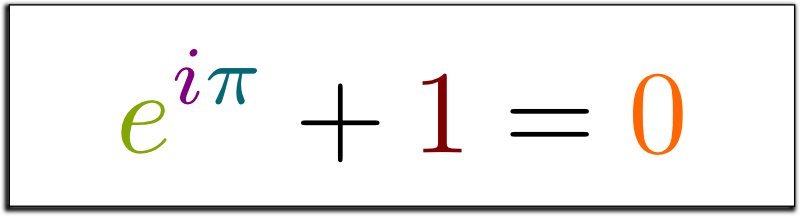Understanding Euler’s Identity - One of the Most Beautiful Mathematical Formulas

Complex Numbers - A Simple Explanation

Complex numbers may seem like an advanced mathematical concept but they have a very intuitive geometric interpretation that makes them easier to grasp. Imagine any polynomial where the coefficients are real numbers. We can express it as the product of two polynomials, where one is the constant term and the other contains the remaining terms. We define a complex number as a polynomial where these two polynomials are considered equivalent. In school, we learned about numbers lying on a number line. Complex numbers extend this idea by existing in a two-dimensional plane. While difficult concepts like square roots of negative numbers are involved, complex numbers allow for a more complete description of rotational motions and oscillations which are prevalent in nature.

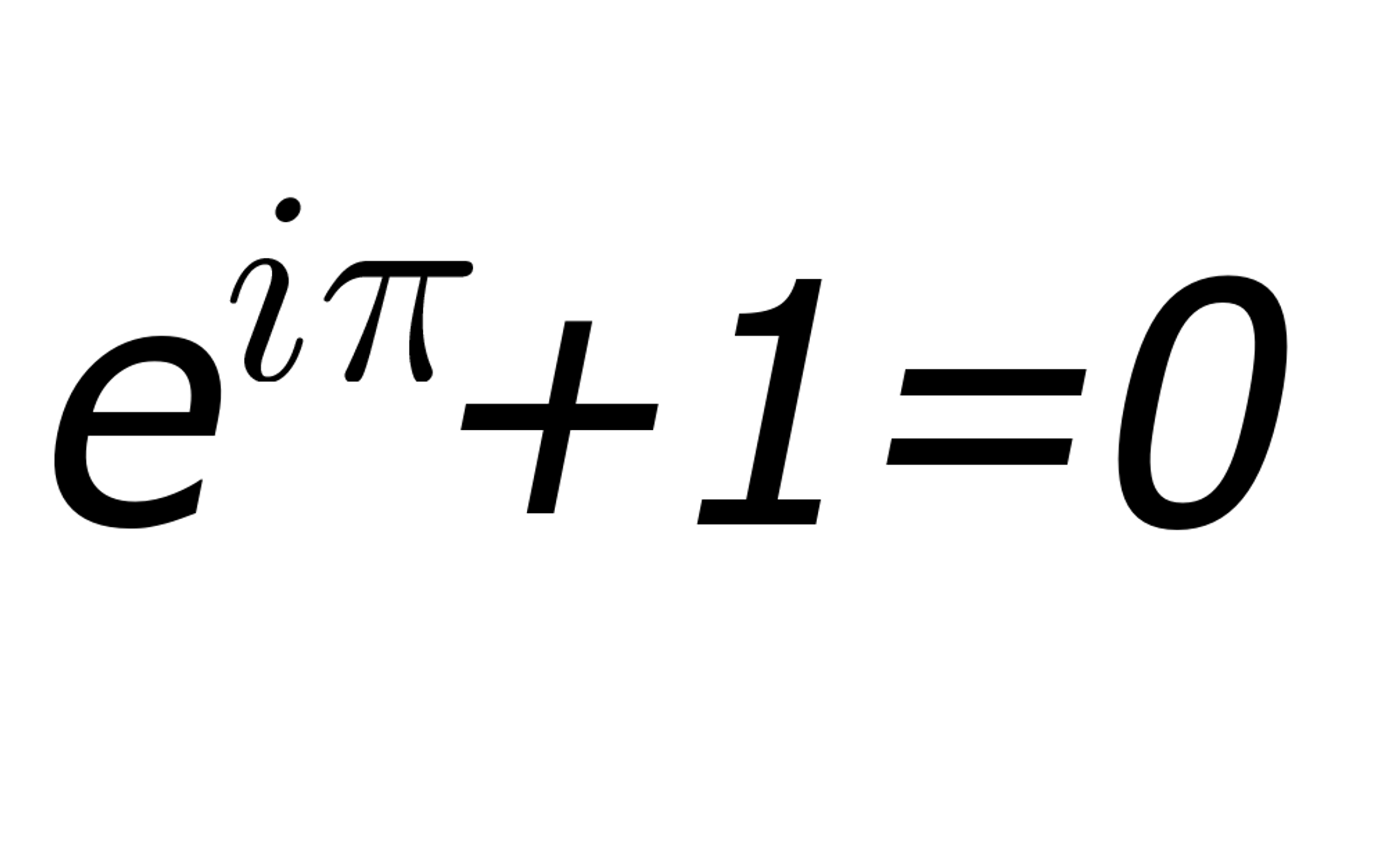
Representing Complex Numbers on an Argand Diagram

To better visualize complex numbers, mathematicians invented Argand diagrams. On these diagrams, the horizontal axis represents the real part of a complex number while the vertical axis represents its imaginary part. Now any complex number can be represented as a single point in this two-dimensional plane. Operations like addition and multiplication of complex numbers translate to geometric transformations on the Argand plane. For example, multiplying a complex number by i results in a 90° counter-clockwise rotation. This simple yet profound connection between complex algebra and Euclidean geometry forms the foundation of mathematical fields like signal processing and control systems.

Exponential Functions of Complex Arguments

The exponential function with real exponents, e^x, plays a central role in calculus and analysis. But does it make sense for the argument x to be complex? Surprisingly, the power series definition of the exponential function can be extended to complex numbers in a natural way. Using techniques like writing complex numbers in polar form, one can show that e^ix must be of the form cos(x) + i*sin(x). This beautiful result, known as Euler’s formula, connects complex exponentials to trigonometric functions and forms the basis of analog signals and quantum mechanics. It was a major breakthrough in understanding the interplay between algebra and analysis on the complex plane.

Deriving Euler’s Identity Step-by-Step

To arrive at the most beautiful of all mathematical formulas, we start from Euler’s formula relating the exponential and trigonometric functions. Simply put x = π in e^ix = cos(x) + i*sin(x) to get e^iπ + 1 = 0. But why should this bizarre-looking identity be true? Let’s examine the reasoning step-by-step:

• Express exponentials of complex arguments as a power series
• Use properties like i^2 = -1 to group real and imaginary terms
• Take the limit of this power series as the number of terms increases
• Relate the limiting behavior to trigonometric function definitions
• Specialize to the case when the argument is π This rigorous derivation reveals the deep interconnections between complex analysis, algebra, and geometry - collectively known as “the face of god” by the brilliant mathematician Euler.

  A Geometric Interpretation of Euler’s Formula

  To gain further intuition, let’s reinterpret Euler’s formula e^ix = cos(x) + i*sin(x) geometrically using Argand diagrams.

• View e^ix as a vector of magnitude 1 rotating uniformly in the complex plane.
• Its real part cos(x) gives the x-coordinate and imaginary part i*sin(x) the y-coordinate.
• Over one complete rotation by 2π radians, this vector traces out the unit circle.
• Hence e^ix provides a natural way to parametrize points on the unit circle! This tells us that complex exponentials are intimately related to rotations, a key unifying concept across science and engineering domains involving oscillations. Furthermore, it sheds new light on why Euler’s identity involves the circle-tracing angle of π radians.

  Applications of Euler’s Formula and Identity

  Armed with this geometric understanding, we can now appreciate profound applications of Euler’s breakthrough:

• Signal processing: Digital signals may be expressed as a sum of complex exponential harmonics using the Fourier transform. This follows from writing sinusoids as real parts of complex exponentials.
• Quantum mechanics: The time-dependence of quantum mechanical wavefunctions is given by e^-iEt/ħ>, connecting energy E to frequency via Planck’s constant ħ. This leads directly to the de Broglie wavelength theory.
• Electromagnetism: Maxwell’s equations take a simple and elegant form using vectors and operators acting on complex electromagnetic field vectors E = E0e^i(kz-ωt). Truly, Euler’s formula and identity opened doors to some of the deepest insights of modern physics. Their import was summarized aptly by the great physicist J. Clerk Maxwell - “This is one of the greatest discoveries in the history of mathematics.”

  Proving Euler’s Identity Using Limits

  So far we’ve seen intuitive explanations, but can we prove Euler’s identity rigorously? Returning to first principles:

• The power series for e^x converges for all real and complex x, not just real x.
• Substitute ix for x and use properties like i^2 = -1 to group real and imaginary terms.
• Taking the limit as the number of terms grows, the real and imaginary parts give cos(x) and sin(x) respectively.
• Finally, plug in x = π to arrive at the iconic formula e^iπ + 1 = 0. This limiting argument establishes the formula on sound mathematical footing. It shows how complex analysis elegantly connects functions originally defined only for real variables. Such limit-based proofs are the bread and butter of mathematical reasoning.

  Closing Thoughts

  Euler’s formula and identity continue to astonish mathematicians with their simplicity and far-reaching implications. They provide a prime example of how pushing conceptual boundaries, even in seemingly clear-cut domains like functions and exponents, can unlock profound surprises. While complex numbers may initially seem esoteric, appreciating their geometric interpretation helps make them intuitively graspable. I hope this guided tour has conveyed some of the unique blend of art and logic underlying this “most beautiful” of mathematical ideas. Its astounding fruitfulness across science is a testament to the deep connections woven into the fabric of mathematics.